レイトレーサーを作るシリーズ:
屈折ベクトル\(\vec{r}\)は、\(\vec{n}\)を法線ベクトル、\(\vec{e}\)を法線と垂直のベクトルとすると
$$ \vec{r} = \vec{e} \sin \theta_2 - \vec{n} \cos \theta_2 $$
光が屈折率の異なる物質に入射するとき、入射する光の角度と出て行く角度の間にスネルの法則:
$$ \eta_1 \sin \theta_1 = \eta_2 \sin \theta_2 $$
が成り立つ。
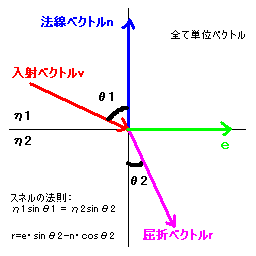
また 、\(\cos \theta_1 = (-\vec{v}) \cdot \vec{n}\)、\(\vec{e} = \frac{\vec{v} - (\vec{v} \cdot \vec{n}) \vec{n}}{\sin \theta_1}\)、 よって屈折ベクトル\(\vec{r}\)は
$$ \begin{align*} \vec{r} &= \vec{e} \sin \theta_2 - \vec{n} \cos \theta_2 \\ &= \left( \frac{\vec{v} - (\vec{v} \cdot \vec{n}) \vec{n}}{\sin \theta_1} \right) \left( \frac{\eta_1}{\eta_2} \sin \theta_1 \right) - \vec{n} \sqrt{1 - \sin ^2 \theta_2} \\ &= \left( \vec{v} - (\vec{v} \cdot \vec{n}) \vec{n} \right) \left( \frac{\eta_1}{\eta_2} \right) - \vec{n} \sqrt{1 - \left( \frac{\eta_1}{\eta_2} \sin \theta_1 \right)^2} \\ &= \frac{\eta_1}{\eta_2} \left( \vec{v} - (\vec{v} \cdot \vec{n}) \vec{n} \right) - \vec{n} \sqrt{1 - \left( \frac{\eta_1}{\eta_2} \right)^2 \left( 1 - \cos ^2 \theta_1 \right)} \\ &= \frac{\eta_1}{\eta_2} \left( \vec{v} - (\vec{v} \cdot \vec{n}) \vec{n} \right) - \vec{n} \sqrt{1 - \left( \frac{\eta_1}{\eta_2} \right)^2 \left( 1 - \left( \vec{v} \cdot \vec{n} \right)^2 \right)} \\ \end{align*} $$
- 屈折率は、ダイヤモンドの 2.417 にしてみた
- 手抜きで球の表面から入るときだけじゃなくて出るときにもちゃんと屈折させないとそれらしくならなかった
- 画角を60度に変えたり
- HLSLにはrefractという組み込み関数がある。全反射で屈折できなかったらどうするんだろうと少し心配。