フレネル反射

2010-03-12
#graphics

fresnel

屈折率\(\eta_i\)の物質から入射角\(\theta_i\)で屈折率\(\eta_t\)の物質に入るときの反射率はフレネル方程式で求められる。 入射面に対する光の平行成分の反射率は\(r_{||} = \frac{\eta\cos\theta_i - \cos\theta_t}{\eta\cos\theta_i + \cos\theta_t}\) 、直交成分の反射率は\(r_{\perp} = \frac{\cos\theta_i - \eta\cos\theta_t}{\cos\theta_i + \eta\cos\theta_t}\) となる、らしい。 偏光されてない光の場合の反射率\(k_r\)は\(k_r = \frac{1}{2}\left(r_{||}^2 + r_{\perp}^2\right)\)となる(sqrtいらないの？)。

\(\eta\)は\(\eta = \frac{\eta_{t}}{\eta_{i}}\)、屈折して出て行く角度\(\theta_t\)のcosは\(\cos\theta_t = \sqrt{1 - \frac{1}{\eta^2}\left(1 - \cos^2\theta_i\right)}\)で求められる。

float fresnel_reflectance(float cos_theta_i, float eta_i, float eta_t) {
  float eta = eta_t / eta_i;
  float D = 1.0 - 1.0 / sq(eta) * (1.0 - sq(cos_theta_i));
  if (D >= 0) {
    float cos_theta_t = sqrt(D);
    float rp = (eta * cos_theta_i - cos_theta_t) / (eta * cos_theta_i + cos_theta_t);
    float rs = (cos_theta_i - eta * cos_theta_t) / (cos_theta_i + eta * cos_theta_t);
    float kr = 0.5 * (sq(rp) + sq(rs));
    return kr;
  } else {
    return 1.0;
  }
}

Balls under water

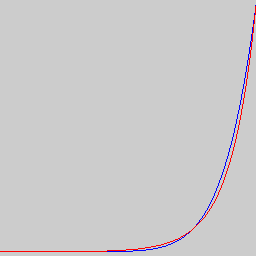
よくやるSchlickの近似は\(k_r \simeq F_\theta + (1 - F_\theta)(1 - \cos\theta_i)^5 , F_\theta = \frac{(\eta - 1)^2}{(\eta + 1)^2}\)

error

個人的には、フレネル反射って効果がいまいち微妙であまりありがたみわからないんだよね…。

関連記事

新着記事